Circadian Rhythm Phase Shift

Shift in circadian rhythm (hours; shift) in three light treatments (treatment).

Usage

JetLagKnees

Format

A data frame with 22 observations on the following 2 variables.

treatment

a factor with levels control, eyes, and knee

shift

a numeric vector

Source

inferred from Wright, K.P., Jr. and C.A. Czeisler 2002. Absence of circadian phase resetting in response to bright light behind the knees. Science 297: 571.

References

http://www.sciencemag.org/cgi/content/full/297/5581/571

Examples

demo(sec15.1)
#> 
#> 
#> 	demo(sec15.1)
#> 	---- ~~~~~~~
#> 
#> > ### JetLagKnees
#> > 
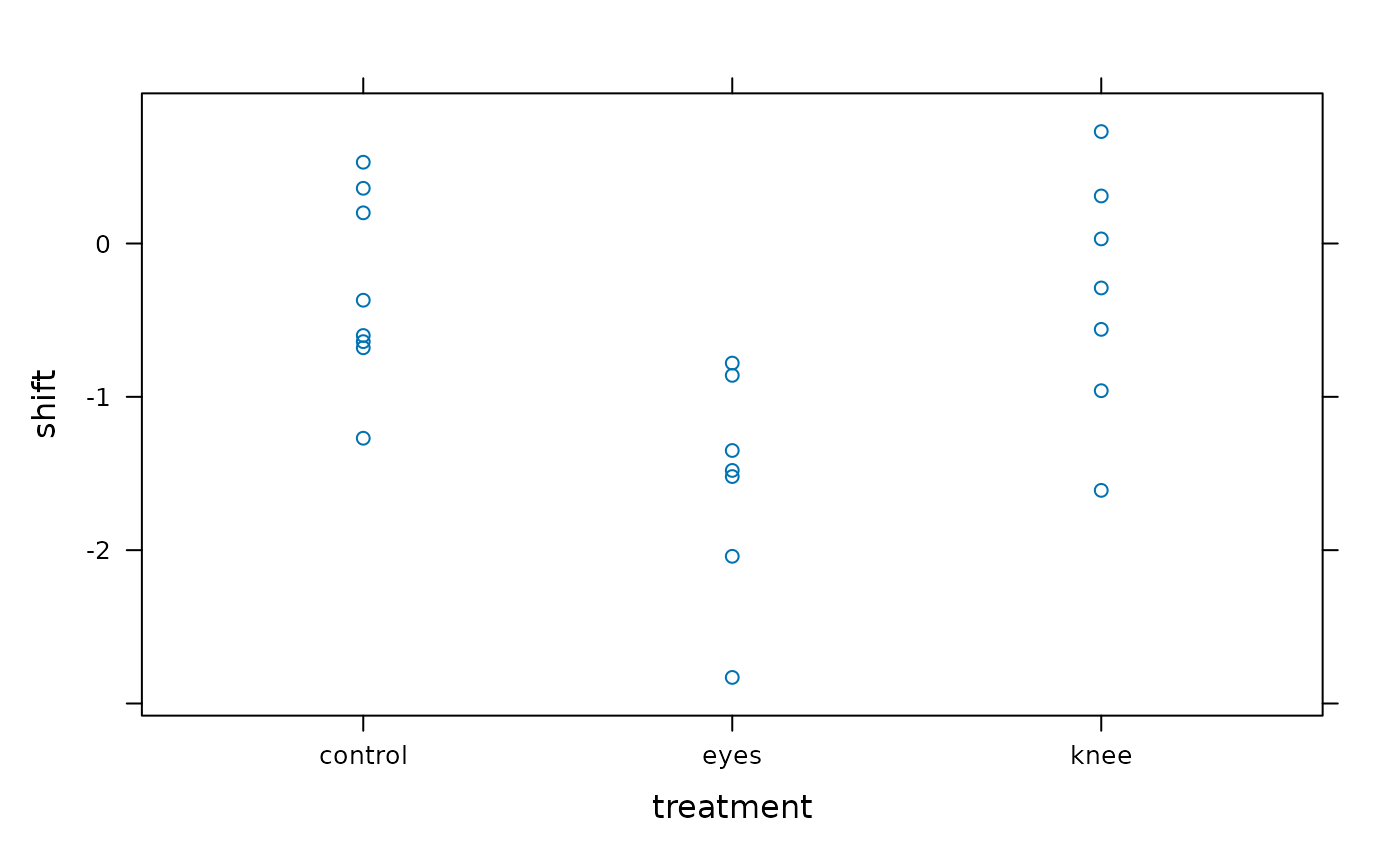
#> > # Approximate Figure 15.1-1
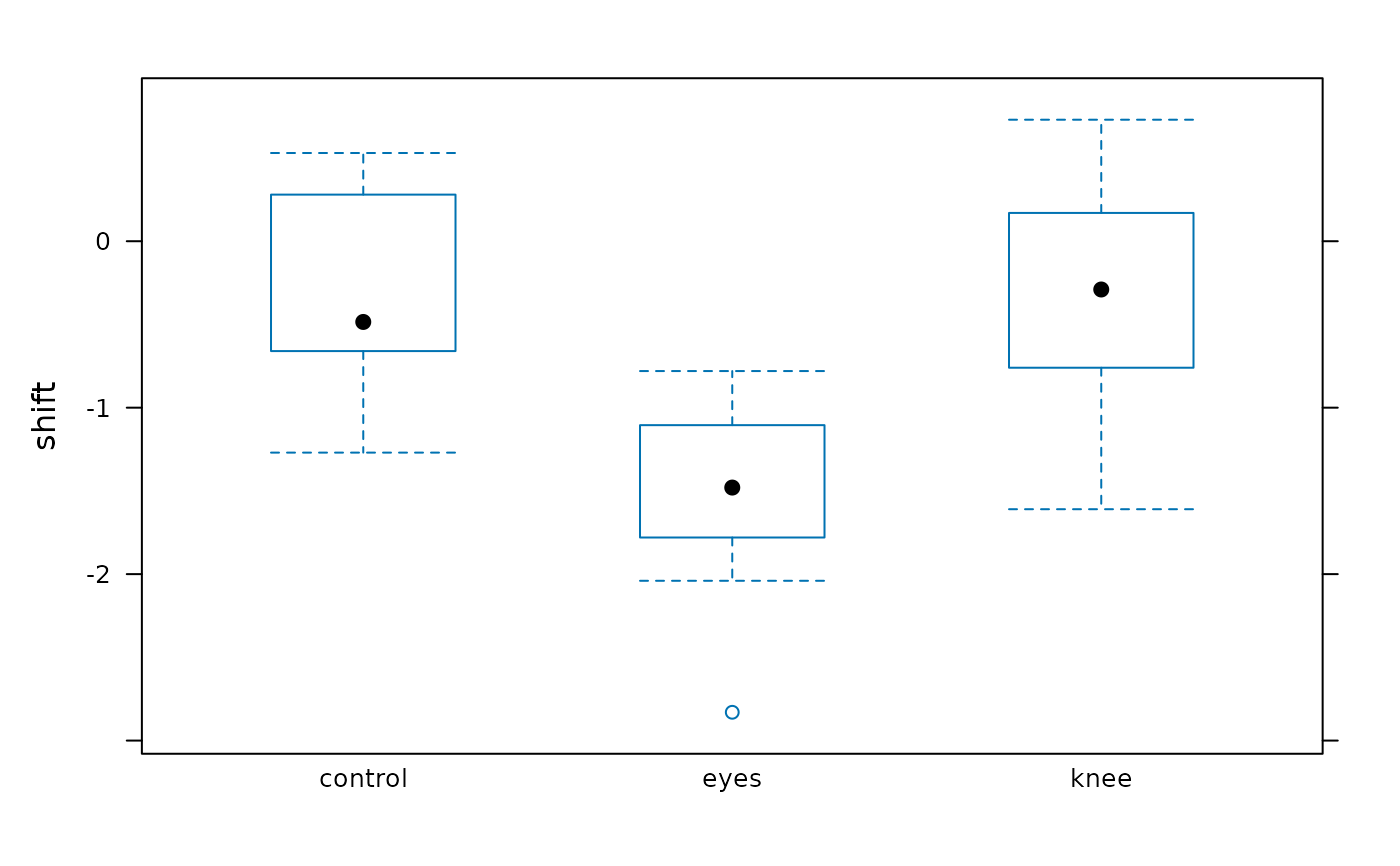
#> > xyplot(shift ~ treatment, data = JetLagKnees)

#> 
#> > bwplot(shift ~ treatment, data = JetLagKnees)

#> 
#> > # Table 15.1-1
#> > if (require(plyr)){
#> +   smry <- ddply(JetLagKnees, .(treatment),
#> +                 function(x)c(Mean = mean(x$shift),
#> +                              s = var(x$shift),
#> +                              n = length(x$shift)))
#> +   print(smry)
#> +   
#> +   # Grand mean
#> +   weighted.mean(smry$Mean, smry$n)
#> + }
#>   treatment       Mean         s n
#> 1   control -0.3087500 0.3813839 8
#> 2      eyes -1.5514286 0.4988810 7
#> 3      knee -0.3357143 0.6253952 7
#> [1] -0.7127273
#> 
#> > # Subset the three treatment groups
#> > control <- subset(JetLagKnees, treatment == "control")$shift
#> 
#> > knee <- subset(JetLagKnees, treatment == "knee")$shift
#> 
#> > eyes <- subset(JetLagKnees, treatment == "eyes")$shift
#> 
#> > # k is the number of groups
#> > k <- length(unique(JetLagKnees$treatment))
#> 
#> > # Calculate n
#> > n <- length(JetLagKnees$shift)
#> 
#> > control.n <- length(control)
#> 
#> > knee.n <- length(knee)
#> 
#> > eyes.n <- length(eyes)
#> 
#> > # Calculate standard deviations
#> > control.sd <- sd(control)
#> 
#> > knee.sd <- sd(knee)
#> 
#> > eyes.sd <- sd(eyes)
#> 
#> > # Error mean square
#> > (SS.error <- ((control.sd^2 * (control.n - 1)) +
#> +   (knee.sd^2 * (knee.n - 1)) +
#> +   (eyes.sd^2 * (eyes.n - 1))))
#> [1] 9.415345
#> 
#> > (MS.error <- SS.error / (n - k))
#> [1] 0.4955445
#> 
#> > # Grand mean
#> > (grand.mean <- (control.n * mean(control) + knee.n * mean(knee) + 
#> +   eyes.n * mean(eyes)) / n)
#> [1] -0.7127273
#> 
#> > # Group mean square
#> > (SS.groups <- (control.n * (mean(control) - grand.mean)^2) +
#> +   (knee.n * (mean(knee) - grand.mean)^2) +
#> +   (eyes.n * (mean(eyes) - grand.mean)^2))
#> [1] 7.224492
#> 
#> > (MS.groups <- SS.groups / (k - 1))
#> [1] 3.612246
#> 
#> > # F
#> > (F <- MS.groups / MS.error)
#> [1] 7.289449
#> 
#> > # P-value
#> > pf(F, 2, 19, lower.tail = FALSE)
#> [1] 0.004472271
#> 
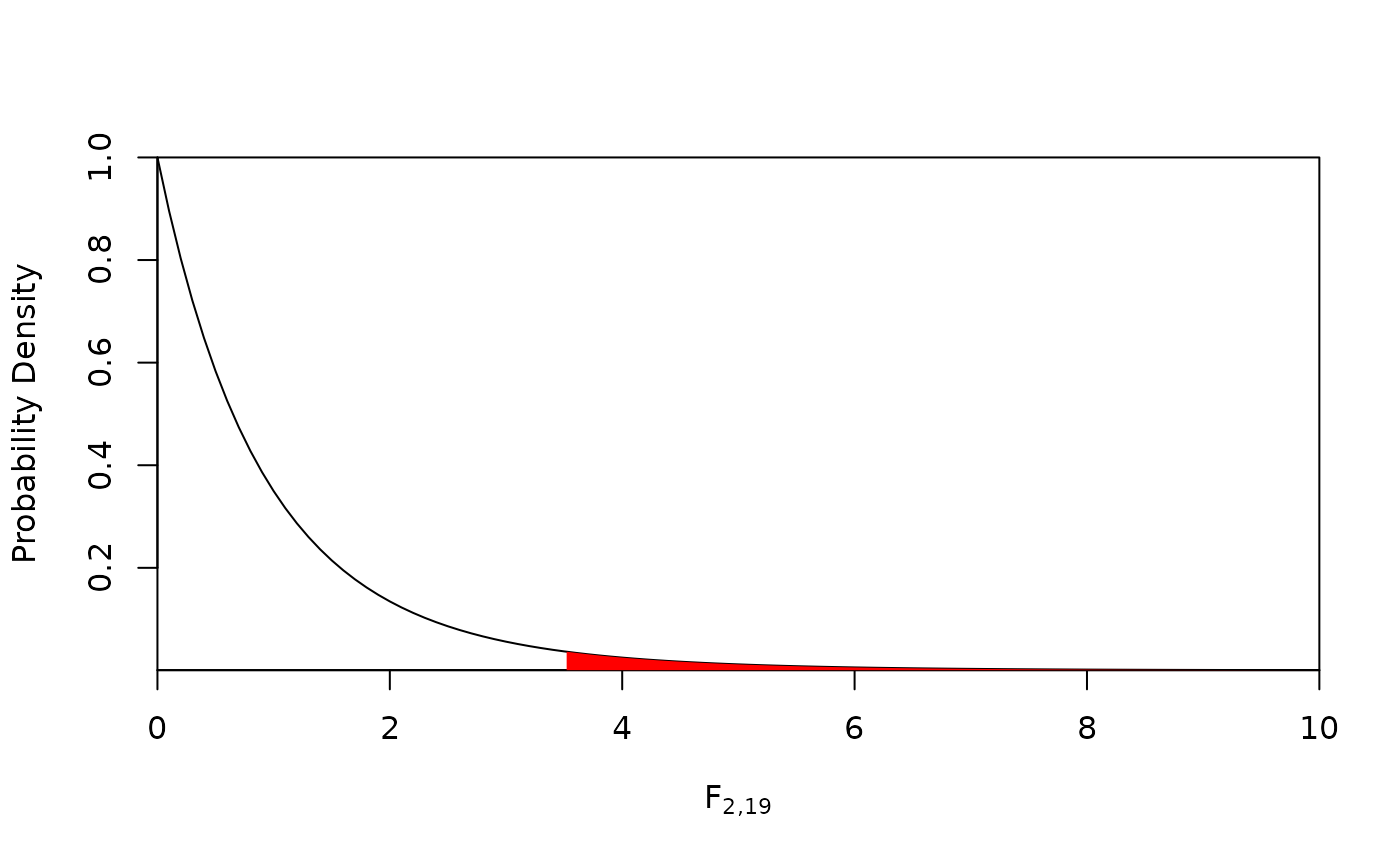
#> > # Figure 15.1-3
#> > (fcrit <- qf(0.05, 2, 19, lower.tail = FALSE))
#> [1] 3.521893
#> 
#> > curve(df(x, 2, 19), from = 0, to = 10,
#> +       ylab = "Probability Density", 
#> +       xlab = expression(F[paste("2,19")]),
#> +       xaxs = "i", yaxs = "i")

#> 
#> > x <- seq(fcrit, 10, length = 100)
#> 
#> > y <- df(x, 2, 19)
#> 
#> > polygon(c(x[1], x, x[100]), c(0, y, df(10, 2, 19)),
#> +         col = "red", border = NA)
#> 
#> > # R^2
#> > (SS.total <- SS.groups + SS.error)
#> [1] 16.63984
#> 
#> > SS.groups/SS.total
#> [1] 0.4341684
#> 
#> > # With aov()
#> > aov.obj <- aov(shift ~ treatment, data = JetLagKnees)
#> 
#> > summary(aov.obj)
#>             Df Sum Sq Mean Sq F value  Pr(>F)   
#> treatment    2  7.224   3.612   7.289 0.00447 **
#> Residuals   19  9.415   0.496                   
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1