Johnson-Neyman Technique

jnt(
  dat1,
  dat2 = NULL,
  which.is.fact = NULL,
  alpha = 0.05,
  total.comp = 1,
  use_sma = FALSE,
  silent = FALSE
)

Arguments

dat1	`data.frame` containing data set 1
dat2	`data.frame` containing data set 2
which.is.fact	Currently not implemented
alpha	Desired alpha level for comparison
total.comp	Total number of comparisons
use_sma	Boolean; use standardized major axis regression
silent	Suppress messages

Value

A list of type jnt containing:

dat1

Data set 1

dat2

Data set 2

alpha

Alpha level

slope1

Slope for data set 1

int1

intercept for data set 1

slope2

Slope for data set 2

int2

intercept for data set 2

lower

Lower edge of range of no significant different in slopes

upper

Upper edge of range of no significant different in slopes

Details

This function performs the Johnson-Neyman Technique on data contained in two data.frames. Currently only the method for data.frames is implemented.

References

Johnson PO and Neyman J (1936) Tests of certain linear hypotheses and their application to some educational problems. Statistical Research Memoirs 1: 57-93.

Hunka S and Leighton J (1997) Defining Johnson-Neyman regions of significance in three-covariate ANCOVA using Mathematica. Journal of Educational and Behavioral Statistics 22: 361-387.

White CR (2003) Allometric analysis beyond heterogenous regression slopes: Use of the Johnson-Neyman Technique in comparative biology. Physiol Biochem Zool 76: 135-140.

Examples:

White CR (2003) The influence of foraging mode and arid adaptation on the basal metabolic rates of burrowing mammals. Physiol Biochem Zool 76: 122-134.

Lavin SR, Karasov WH, Ives AR, Middleton KM, Garland T (2008) Morphometrics of the avian small intestine compared with that of nonflying mammals: A phylogenetic approach. Physiol Biochem Zool 81: 526-550.

Author

Kevin Middleton (middletonk@missouri.edu)

Examples


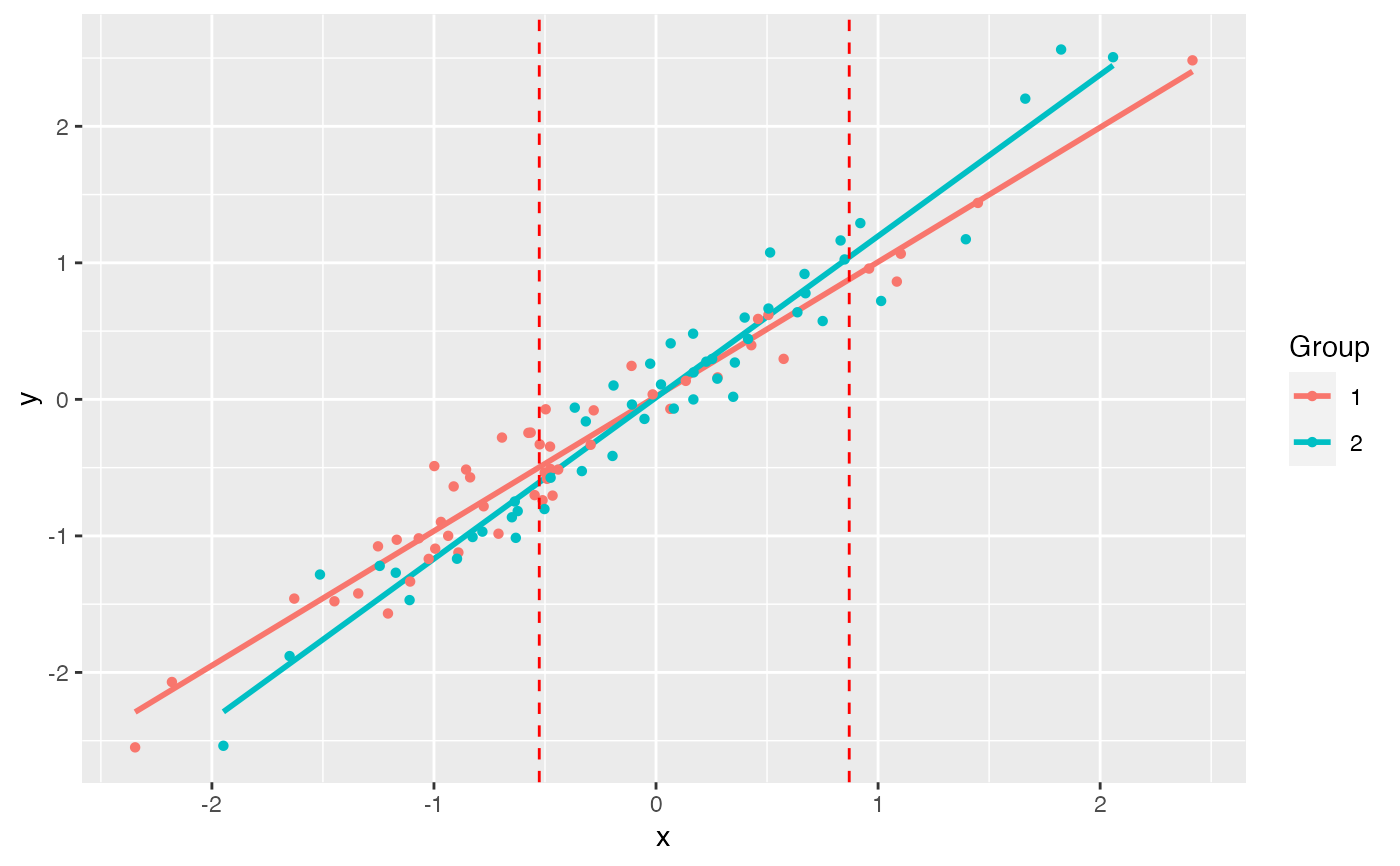
# Simulate data
set.seed(1234)

n <- 50

x1 <- rnorm(n)
y1 <- x1 + rnorm(n, sd = 0.2)

x2 <- rnorm(n)
y2 <- 1.25 * x2 + rnorm(n, sd = 0.2)

df1 <- data.frame(x = x1, y = y1)
df2 <- data.frame(x = x2, y = y2)

(jnt.out <- jnt(df1, df2))
#> Fitting with OLS
#> Assuming x variable is column 1, and y is column 2.
#> 
#> Johnson-Neyman Technique
#> 
#> Alpha =  0.05 
#> 
#> Data 1:
#> 	Slope		 0.9853 
#> 	Intercept	 0.02126 
#> 
#> Data 2:
#> 	Slope		 1.182 
#> 	Intercept	 0.01386 
#> 
#> Region of non-significant slope difference
#> 	Lower: -0.5258 
#> 	Upper: 0.8701 
#> 

plot(jnt.out)
#> `geom_smooth()` using formula 'y ~ x'